Operating at High Cant Deficiency

by Peter Klauser • October 2005

Cant deficiency has a significant effect on curving performance of vehicles in both passenger and freight service. The forces due to centrifugal acceleration through a curve must ultimately be reacted at the wheel/rail interface. Curve lateral acceleration and the compensating effect of track superelevation can be expressed mathematically as shown in Figure 1.

At a specific speed, termed the balance speed, the compensation due to superelevation balances the acceleration due to curving. Relative to the track plane, the perceived lateral acceleration is then zero. At speeds under the balance speed, the lateral acceleration term is less than the superelevation term. This is termed cant excess, meaning the track has excessive cant for the present speed. At speeds over the balance speed, the lateral acceleration term is greater than the superelevation term. This is termed cant deficiency, meaning the track has insufficient cant for the present speed. With cant deficiency, perceived accelerations are to the outside of the curve; with cant excess, perceived accelerations are to the inside of the curve.

Cant deficiency or excess is often expressed as an amount of insufficient or excess superelevation—inches of cant deficiency. They can also be expressed as uncompensated acceleration—in ft/sec². As a conversion, 1 inch of cant deficiency corresponds to just over 1/2 ft/sec² of uncompensated lateral acceleration.

The left side of Figure 1 shows a rail vehicle on a superelevated curve. The vehicle body is actively tilted toward the inside of the curve, giving passengers a perception of greater superelevation and thus lower perceived lateral accelerations. Without a tilt system, the vehicle body would generally roll towards the outside of the curve with cant deficiency and towards the inside of the curve with cant excess. From the view of passenger comfort, these rotations are in the wrong direction and cause the passenger to perceive even greater lateral accelerations. If the center of rotation of the suspension system can be placed above the body center of gravity, the body will roll inward under cant deficiency. This creates a passive tilt system. The Talgo trains operating in the Pacific Northwest are an example of this design.

What are typical limits on cant deficiency or excess? For cant excess, the worst case is a stationary train. The cant excess limit is equivalent to the maximum allowable superelevation. The cant deficiency limit is typically dictated by maximum uncompensated lateral acceleration, rather than derailment safety. Safe operation is possible at much higher cant deficiency levels than trains usually encounter. Tilting trains prove this by operating at cant deficiencies two to four times those of conventional trains. Operation is safe, as evidenced by non-tilting power cars or locomotives.

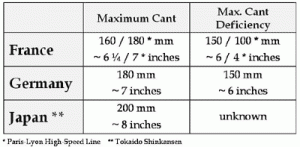
Figure 2 shows representative cant limits for operations in three countries, France, Germany and Japan, which have well-established high-speed rail systems. France and Germany have maximum superelevation levels equal to the FRA limit of 7 inches. Japan is marginally higher at 8 inches. For cant deficiency, all three countries allow higher values than the 3 inches accepted in the U.S. (in the absence of an FRA waiver). On conventional lines, France and Germany allow operation with up to 6 inches cant deficiency. On TGV high-speed lines in France, the limit is 4 inches, in part because of the very large curve radii on such lines. Thus there is no requirement to go to higher cant deficiency.

High-Speed Curving Issues

For passenger trains, the primary high-speed curving issue is lateral acceleration. Rail passengers expect to safely and comfortably stand up and walk around during their journey. Standing passengers are thus the worst case. Accelerations on the order of 3-4 ft/sec² are generally the maximum acceptable.

Passenger comfort in curves can be improved by tilting the vehicle body. This reduces the perceived lateral acceleration, thus allowing higher curve speeds. The first tilting train was the Advanced Passenger Train (APT) in the U.K. This design was unsuccessful, principally due to project management, rather than technology. Successful designs, coming 10 years later, were the X2000 in Sweden and the Pendolino in Italy. The Pendolino is a clear commercial success with trains delivered to nearly a dozen countries. Tilt trains of various designs are now used in almost 20 countries. The Acela trainsets are a domestic example.

Figure 3 shows a Pendolino train running through an S curve (note that each car tilts independently). The tilt mechanism is a pair of hydraulic cylinders and inclined links on each truck. These act to rotate the car about a point 60 to 70 inches above top of rail. This corresponds roughly to passenger head or chest level. Experience has shown this roll center maximizes perceived comfort. Tilt trains typically run at maximum uncompensated accelerations of 5-6 ft/sec² with 60% to 70% compensation. Full compensation leads to greater discomfort. Passengers want some perception of curving, otherwise visual and inner ear signals conflict, leading to motion sickness.

Safety-related issues must also be addressed. What is the derailment risk at high cant deficiency? Are the lateral forces guiding the vehicle sufficient to cause it to leave the track, perhaps even overturn? Inversely, are the lateral forces large enough to cause track shift? Some of these issues will be illustrated by modeling results for a vehicle patterned after the newest generation Pendolino. The calculations were done using the VAMPIRE® vehicle dynamics model.

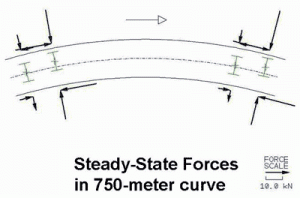
Figure 4 shows steady-state curving forces at balance speed in a 750-meter curve (nearly 2-1/2 degrees). The arrows depicting lateral forces are normal to the arc representing the curve. The arrows depicting longitudinal forces are tangential. The lateral forces are the force of the rail on the wheel.

For both the outside and inside curve rails these forces are directed towards the track center. This means the wheels are attempting to spread the gauge and the rails are resisting. Gauge-spreading forces are large at the leading axle and minor at the trailing axle. The axle steering moment is large at the leading axle and relatively small and in the opposite direction at the trailing axle. The leading and trailing truck patterns are similar.

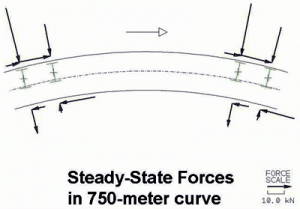
Figure 5 shows curving forces at 12 inches cant deficiency. Changes at the truck leading axles are minor, while trailing axle changes are dramatic. The trailing axle now takes an equal role in generating truck lateral forces. Gauge spreading no longer occurs at the trailing axle. Instead, the low rail wheel now acts to pull the low rail towards track center. The steering moment on the leading axle is largely unchanged, while the steering moment on the trailing axle has changed sign.

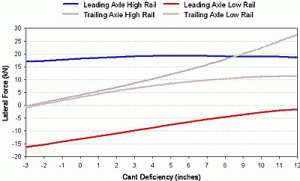
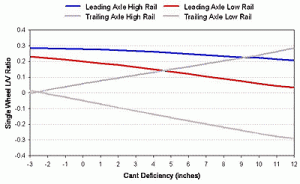
Figure 6 shows how truck lateral forces are affected by cant deficiency. At the leading axle, high rail lateral forces hardly change. The required increase in net axle lateral force at high cant deficiency is obtained by reducing forces at the low rail.

These go from a larger negative value to a smaller negative value. There are also substantial increases in lateral force on the trailing axle. While it is typically assumed that high-speed curving causes significant high rail loads, it is actually the low rail forces that change most to create the net lateral load as the vehicle reacts to centrifugal force.

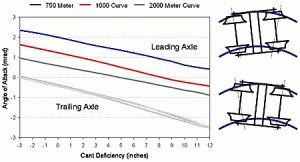
Wheelset angles of attack decrease with increased cant deficiency. The diagram at the top right of Figure 7 shows the usual curving orientation of a truck at balance speed. The leading axle takes an angle of attack and the trailing axle takes a near-radial position. The bottom right diagram shows the curving orientation at high cant deficiency. In this condition, the leading axle moves into a radial position (the angle of attack decreases) while the trailing axle goes to an over radial position. This has important consequences in terms of derailment safety.

Derailment Risk

The first issue with regard to derailment is wheel climb. The high rail/leading axle L/V ratio tends to decrease with increasing cant deficiency. Lateral loads do not increase substantially, while vertical loads do (load shifts from low rail to high rail). The trailing axle L/V ratio for the high rail increases substantially.

The effect of angle of attack should also be considered when analyzing the potential for wheel climb. The Nadal criterion for wheel climb is very conservative at low or negative angles of attack. Under these conditions the critical L/V ratio can be several times greater than the Nadal limit. At high cant deficiency, the leading axle, which is critical in terms of derailment risk, has a near-radial alignment. The trailing axle, which may in fact have a higher L/V ratio, is in an over-radial position and thus effectively cannot derail.This is because the lateral load increases substantially. However, relative to conservative safety criteria, the L/V ratios are not substantial.

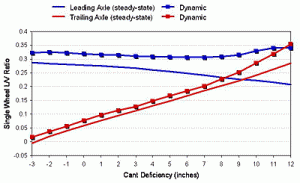
Figure 8 shows quasi-static values over perfect track, while Figure 9 shows dynamic values predicted over measured track geometry. The high rail values increase most due to dynamic response. This is the result of flange contact and track irregularities on the high rail.

The true derailment risk at high cant deficiency comes from the fact the vehicle attempts to push the track out from under itself. The safety issue is closely related to track buckling. High-speed trains may encounter speed restrictions during extremely hot weather. Greater track longitudinal forces due to temperature and greater net axle lateral forces due to cant deficiency increase the risk of track buckling.

The critical value is the net axle lateral load. In Europe, the limit is defined by the Prud’homme formula. Track lateral strength is defined by a constant term and a term linearly dependent on axle load. Relative to axle load, maximum track strength is obtained at low axle loads. Tilting vehicles intended for high cant deficiency thus have comparatively low axle loads, on the order of 15 tons to 20 tons maximum per axle. The current U.S. standard is solely proportional to axle load. However, current discussions and research findings will probably move the U.S. to adopt a limit similar in form to thePrud’homme formula.

The final safety concern is vehicle overturning. At high cant deficiency, lateral forces may be sufficient to cause unloading of the low rail wheels and possible vehicle overturning. This is particularly an issue for vehicles with high centers of gravity operating with high winds. Speed restrictions may be required for high-speed trains during high wind periods.

A last observation with regard to cant deficiency is that curving resistance drops with increasing speed. This is true, dependant on curve radius, to roughly 3 – 5 inches cant deficiency. The optimum from the view of curve resistance and rail and wheel wear is to generally operate at maximum speed.

So what is the relevance to freight service of operation at high cant deficiency? Curves on freight lines typically have excess superelevation. This is perhaps a legacy of past passenger train operations. As a result, trains tend to operate at cant excess, rather than cant deficiency. A reduction in superelevation would move freight trains to operating at balance speed or slightly above balance speed. This change would be accompanied by small but nonetheless realizable benefits. One is a reduction in low rail plastic deformation. Operating at cant excess shifts the load to the low rail. Since hollow-worn wheels generate large contact stresses on the rail field side, crushing, plastic flow, and surface defects are likely consequences. Operating at balance speed or slight cant deficiency reduces these effects. There is also potential for a reduction in total wheel and rail wear.

Finally, there is a reduction in gauge-widening force. Operating at cant deficiency reduces the low rail lateral load more than it increases the high rail lateral load. Thus, the net gauge-spreading load will be reduced. Since low rail rollover is generally of greater concern than high rail rollover, reducing the lateral load on the low rail is a further benefit.

In passenger service, carbody tilt has virtually no effect on wheel/rail forces, but has a substantial effect on passenger comfort. The U.S. cant deficiency limit of 3 inches is overly conservative. Conventional passenger trains could operate at 5% to 10% higher curve speeds without affecting passenger comfort or safety. Extreme cant deficiency results in curving behavior that is uncharacteristic, or outside the generally accepted scheme of curving forces. Single wheel L/V ratios are not the critical issue for high-speed curving. Instead, track panel shift and vehicle overturning, particularly under high wind conditions, are critical.

For freight service, reducing curve superelevation, and thus increasing cant deficiency, can reduce rail wear, particularly low rail plastic flow and fatigue damage. The potential for low rail rollover is also reduced.

This article is based on a presentation by Peter Klauser at Advanced Rail Management’s Wheel/Rail Interaction ’05 Seminar.

Peter Klauser is a Vehicle Dynamics Engineering Consultant