Using Wayside Load Detectors for Preventive Vehicle Maintenance (Part 1 of 2)
By B. McGuire, R. Sarunac, R. B. Wiley and P. Klauser • April, 2007
The use of vehicle performance detectors is steadily growing on North American freight and high-speed passenger railways. With the installation of a Wayside Wheel/Rail Load Detector (WRLD) on the Washington Metropolitan Area Transit Authority (WMATA), the trend now extends to the rail transit industry, as well.
The original truck performance detector (TPD) was developed in the mid-1990s by the Transportation Technology Center, Inc., through the Association of American Railroads’ (AAR) research program. TPDs measure wheel/rail forces via strain gauge sensors on the rails in selected reverse curves. They also can measure the angle of attack of each axle with respect to the rail — a parameter that, in combination with measured vertical and lateral forces, provides information regarding the steering capability of a truck through curves.
TPDs identify suspension systems that do not perform optimally in (or after negotiating) curves. Poor performance may result in derailments due to wheel climb, gauge spreading, rail rollover or track panel shift. Poor performance also contributes to wear on rail, special trackwork, wheel profiles and flanges. By identifying poor performers through performance-based monitoring, preventive maintenance can be performed, reducing derailment risks and improving the overall safety of rail operations.
TPDs are designed to measure rail vehicle curving performance under specific conditions. Measurements (shown in Figure 1) include:
— Vertical Force. The force generated by the wheel perpendicular to the plane of the track.
— Lateral Force. The force generated by the wheel in the plane of the track but perpendicular to the direction of motion.
— Angle of Attack. The angle taken by the axle relative to the direction of motion.
A typical TPD site consists of an “S” curve arrangement where two curves (typically 4 to 6 degrees) are in the opposite direction relative to each other (i.e., a right-hand and a left-hand curve with a tangent section separating them). A modified form of a TPD in the form of a single-curve load station, a Wayside Wheel/Rail Load Detector (WRLD), was installed at WMATA.
Originally, wayside detectors (such as hotbox, wheel impact load and TPDs) were intended for use in exception reporting. Whenever an axle roller bearing temperature, wheel impact or truck performance indicator exceeds a pre-determined threshold, an alarm is raised and the offending item is removed from service at the earliest opportunity. This is the simplest use of wayside detectors.
Within the past few years, TPD data has been used to monitor changes in repeated performance over time and to predict when an alarm condition will be reached. Additionally, the performance profile of a suspected “bad actor” can be compared to peer vehicles or an expected normal performance profile. This allows for prioritization of maintenance plans for the equipment most in need of repair. It also provides a means to declare a vehicle as consistently performing within normal and safe operating ranges for various performance indices, and, thus, not in need of maintenance. In order to accommodate this new approach to performance monitoring, a system, known as InteRRIS®, was designed to process, store, analyze and automatically report on vehicle condition (see Figure 2 next page).
WMATA’s WRLD Project
WMATA, working with a team of engineers from Booz Allen Hamilton, TTCI and the WMATA engineering staff, installed a WRLD at one of its yards to assess vehicle performance and identify poorly performing rail cars. WMATA’s primary objective was to install and modify a WRLD in order to characterize the existing fleet by establishing a database of wheel/rail forces. WMATA also wanted to monitor wheel/rail forces on vehicles that have experienced low-speed flange-climb derailments (and thereby decrease the probability of such incidents), establish a baseline of wheel/rail forces for the newest series rail cars, and compare measured wheel/rail forces with modeling and simulation results. A secondary objective was to pinpoint specific defects based upon vehicle dynamic signatures.
Real-time data collection allowed immediate access to the curving performance of individual rail cars; data was used to assess vehicle dynamic behavior during acceptance testing. Data stored in a database at the WRLD site were accessed via an Internet InteRRIS® link. This data was evaluated for generating performance alarms of poorly performing rail cars — an important project milestone, since gaining maintenance personnel’s confidence in the WRLD’s abilities was one of the major objectives. The system is also used to evaluate specific vehicle types and overall fleet performance.
WMATA’s WRLD determines truck performance by measuring lateral loads, vertical loads and angles of attack (along with lateral to vertical (L/V) load ratios, speed, average car weight and total train weight) as vehicles and trains pass the detector. The WRLD is used to identify and schedule preventive maintenance for poorly performing vehicles. In longer term, early detection of potential “troublemakers” could allow WMATA to transition from scheduled to preventive maintenance.
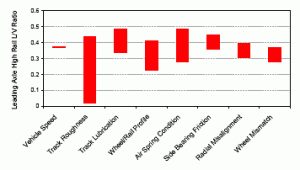
Prior to installing the WRLD, a (VAMPIRE®) simulation was run to predict the angles of attack, lateral and vertical forces, and single wheel L/V ratios that were anticipated at the measurement site. The conditions considered were vertical load, vehicle speed, track roughness, wheel/rail friction, wheel and rail profiles, nominal track gauge, inflated or deflated air springs, air spring pressure imbalance, side bearing coefficient, truck radial misalignment and wheel diameter mismatch. Generally, these factors were considered individually, rather than in combination.
The modeled vehicle was an empty car with a weight of approximately 80,000 pounds. The car length was roughly 75 feet, and the truck center distance was just over 50 feet. The trucks were a two-axle (all powered), two-part frame design with cast side frames and bolster, rubber primary suspension and air spring secondary suspension. The measurement site was a 1,614-foot radius (3.5-degree) curve without superelevation.
Results were based on “nominal case” condition — i.e., empty car weight (AW0), vehicle speed of 15 mph, coefficient of friction (tread and flange) of 0.35, wheel flange angle of 69 degrees, worn rail, standard gauge, perfect track, no air spring imbalance, no wheel mismatch and side bearing coefficient of friction of 0.12. The following parameters were analyzed to determine their impact on performance:
— Vehicle Load. The vehicle load at the current (yard lead) measurement site is unlikely to vary significantly from AW0 (ready-to-run). The effect of greater vehicle load is to increase the axle steering moment. Therefore, a higher vehicle load (AW3 vs. AW0) tends to reduce the single wheel (leading axle, high rail) L/V ratio. This is the result of vehicle interior arrangement (weight imbalance). Because the vehicle speed is above the curve balance speed, the vertical load will shift toward the high rail.
— Vehicle Speed. The vehicle speed for yard track is unlikely to be a completely controllable variable, since the vehicle may pass the measurement site at a range of speeds. For a 1,614-foot radius curve and a speed range of 5 mph to 35 mph, the effect on single wheel (high rail) L/V ratio was found to be insignificant.
— Track Roughness. The impact of track roughness is one of the most influential parameters on vehicle performance. The majority of the simulations that were performed considered a constant radius curve with perfect geometry (i.e., no deviations in curve gauge, crosslevel, alignment or profile from ideal values).
— Wheel to Rail Friction. The wheel/rail friction coefficient is the first critical influence on vehicle curving performance. The simulations involved two friction values: the first for contact between the wheel tread and rail crown, the second for contact between the wheel flange and rail gauge face. Both coefficients were equal with values varying from 0.2 to 0.5. Lubrication reduced the wheel flange coefficient of friction to 0.15; the wheel tread coefficient of friction was either 0.35 or 0.5. Weather conditions and rail contamination are generally outside of operator control; however, wheel or rail lubrication provides a means to provide a controlled friction environment. The angle of attack decreases significantly as wheel/rail friction increases. Also, lubrication tends to increase angle of attack and lateral forces, and reduce axle steering forces. This means that values collected on a rainy day may not be directly comparable to those obtained after an extended period of hot and dry weather.
— Wheel and Rail Profiles. Wheel and rail profiles, the resulting contact geometry and changes due to wear were determined to be the second most critical influential factor. The simulation assumed that wheel wear tends to increase flange angle and reduce tread taper. A greater flange angle is accompanied by some increase in flange clearance. Wear tends to transfer the wheel flange contour to the high rail (consistent flange contact) and wheel tread contour to the low rail (consistent tread contact). High rail wear tends to reduce the rail gauge-face angle, while low rail wear tends to flatten the rail crown. Both effects — increased flange angle and smaller tread conicity (due to reduced tread taper / flange side tapeline wear) — tend to reduce wheelset steering. WMATA’s nominal track gauge, which is 1/4-inch tighter than the North American standard, results in normal tread contact shift toward the flange side of tapeline. The rail is AREMA 115 pound at 1:40 cant; the wheel is a British worn profile (63-degree nominal flange angle) at 1:20 taper. The nominal pairing was a worn wheel with 69-degree flange angle on curve-worn rails at standard gauge. Simulation indicates that both angle of attack and single-wheel L/V ratio tend to increase with flange angle (wheel wear). However, it should be noted that the Nadal limit value for single-wheel L/V ratio increases significantly as flange angle increases, as does the safety margin against wheel climb derailment.
— Air Spring Imbalance. The effect of air spring imbalance was analyzed as the third most critical influential factor. The modeled car was equipped with a four-point leveling system. The disadvantage of this arrangement is the potential for a diagonal air spring load imbalance. In this case, air spring loads and pressures are increased at two diagonal corners and reduced at the opposing corners. The diagonal load imbalance does not create a car pitch or roll imbalance. Instead, the forces are reacted by carbody twist about the length axis. The effect of the diagonal air spring load imbalance is that static vertical loads per truck side are no longer uniform. Instead, truck side vertical loads under static conditions are roughly proportional to the diagonal variation in nominal air spring pressures. A further effect is that air spring stiffness is also roughly proportional to air spring pressure. Thus, the car is supported on a pair of “stiff” springs at two diagonal corners, and a pair of “soft” springs at the opposing corners. Under dynamic conditions, this leads to further reduction in vertical load at the lightly loaded corners. The total air spring imbalance represents a combination of the car’s weight distribution, the static imbalance occurring on a level truck (due to improper adjustment of the car leveling system) and the effect of track twist (i.e., the spiral). In addition to the diagonal imbalance, improper car leveling may result in further static imbalance (car roll) due to uneven air spring height. This illustrates that the air spring condition has significant influence on vehicle curving performance.
— Side Bearing Friction. The effect of side bearing friction coefficient on the curving performance was investigated as a minor causal factor. Investigation indicates that an increase in side bearing friction will proportionally increase truck-turning resistance.
Perhaps unexpectedly, maximum L/V ratios are predicted for the lowest friction value for the trailing truck. An increase in side bearing friction reduces the predicted L/V ratio. The results for the leading truck are the opposite. For a vehicle’s leading truck, the direction of truck rotation and the resulting turning moment increase the lateral force at the leading-axle, high-rail wheel. For a trailing truck, the direction of truck rotation and resulting turning moment are opposite to the leading truck; the turning moment tends to reduce the lateral force at the leading-axle, high-rail wheel. The lower the turning moment, the lower this beneficial effect and the greater the potential for derailment of the leading axle. The influence on single-wheel L/V ratios are not significant. Side bearing friction appears to have limited influence.
— Truck Radial Misalignment and Wheel Mismatch. The impact of truck radial misalignment and wheel mismatch was also investigated. Truck misalignment refers to defects when wheelsets are not parallel. Misalignment values of 1 to 2 milliradians were considered. Wheel diameter mismatch is a defect when the left and right wheels have diameter mismatch. Diameter mismatch of ± 2 mm was considered.
—Radial misalignment strongly influences wheelset angle of attack. The increased angle of attack at the truck leading axle increases wheel lateral forces, leading to the greater single wheel ratios. Negative misalignment of 2 milliradians creates the worst case single-wheel L/V ratio. Angle of attack measurements could provide a means to identify trucks outside the desired geometric tolerances. The single-wheel L/V ratio does not indicate a consistent trend; maximum values occur for the nominal case with zero diameter mismatch. Either negative or positive diameter mismatch tends to reduce the L/V ratio on the leading axle high-rail. This effect is of limited importance, however.
— Track Gauge. A nominal track gauge of 56-1/4 inches for tangent track and curve radii greater than 1,425 feet is used on the WMATA system. This is 1/4 inch tighter than standard gauge. The 56-1/4 inches is increased by 1/2 inch for curve radii less than 1,415 feet. To investigate the influence of nominal track gauge, simulations were made for gauge values ranging from 1/4 inch tight to 1/4 inch wide. Track gauge has been found to have negligible influence on angle of attack, and minor influence on single-wheel L/V ratio. In fact, the single-wheel L/V ratio decreases with wider gauge.
— Findings from Simulations.The simulation results revealed that the average leading axle L/V ratios are less than 0.1 — approximately 0.05 to 0.06 for a “perfect” vehicle. The lead-axle, high-rail L/V ratio appears to be the best approach to differentiate poorly performing cars. High-rail L/V ratios in the range of 0.3 to 0.4 would indicate a vehicle that is steering poorly with hard flange contact, and is running with a lead axle that has a relatively large angle of attack.
![]()
B. McGuire is Quality Assurance Officer in the Quality Assurance Department of System Safety and Risk Management, Washington Metropolitan Area Transit Authority; R. Sarunac is Lead Mechanical Engineer in the Washington, D.C., office of Booz Allen Hamilton; R. B. Wiley is Principal Investigator at the Transportation Technology Center, Inc.; P. Klauser is a Vehicle Dynamics – Engineering Consultant.
Acknowledgements
The authors would like to acknowledge the support and asistance of J. Pringle, T. Consavage, D. Ogunrinde, D. H. Smith and D. George of WMATA, and C. Stuart of Booz Allen Hamilton. Special thanks to A. Coe and M. Hiller of WMATA for providing field assistance and close collaboration in writing this article.
References
5000 Series Rapid Transit Car Technical Specification, WMATA, June 1999.
6000 Series Rapid Transit Car Technical Specification, WMATA, July 2002.
AAR, “Rail Car Train/Track Dynamic Testing,” Report No. P-93-109, March 1993.
Klauser, P., “Curving Performance of WMATA Cars,” February 2005.
Sarunac, R., and Klauser, P., “Effect of Secondary Suspension Air Spring Imbalance on Wheel Climb Derailment Potential,” APTA, Pittsburg, June 2005.
TTCI, “WMATA Wheel-Rail Interface Study,” October 2005.
Zeta-Tech Associates, “Derailment of Transit Vehicles in Special Trackwork,” Final Report, TCRP, July 1996.