Flange Climb and Independently Rotating Wheels

by Bob Tuzik, December 1, 2004

Investigations have shown that wheel-flange/gauge-face angle and the coefficient of friction (COF) play significant roles in contributing to or preventing flange-climb derailments. Investigations have also shown that Light Rail Vehicles with Independently Rotating Wheels (IRWs) have a greater propensity for flange-climb derailment than vehicles with conventional wheelsets and rigid axles. While not an industry-wide issue, this affects a number of transit systems using various types of articulated two-car and articulated three-car low-floor vehicles, which incorporate trucks with IRWs in the center low-floor section of the vehicle.

What are the differences between conventional, rigid axles and IRWs, and why are IRWs more prone to flange-climb derailment?

Figure 1

“Independently rotating wheelsets tend to climb the rail more easily than conventional solid wheelsets due to a lack of self-steering capability,” John Elkins, president of RVD Consulting, Inc., told delegates at Interface Journal and Advanced Rail Management’s Rail Transit ’04 Wheel/Rail Interaction Seminar. Flange climb occurs at lower L/V ratios with IRWs than with conventional wheelsets, and the flange climb distance is shorter for IRWs than for conventional wheelsets, so the L/V must be sustained for a shorter length of time to cause a derailment.

When a conventional wheelset takes an angle of attack, it creates lateral creepage, which generates a lateral force. As the wheelset moves laterally, rolling radius difference generates longitudinal forces, or steering moments, on the wheelset. “The wheel that is larger in radius tries to pull the wheelset forward while the wheel that is smaller in radius tries to pull it back. That creates a turning moment,” Elkins said.

A conventional, rigid-axle wheelset that is in flange contact with an angle of attack generates lateral and longitudinal forces. The longitudinal force will reduce the possible magnitude of the lateral force, he said. “The larger the longitudinal force, the smaller the lateral force can be.”

IRWs, on the other hand, generate no steering moment—even when shifted laterally. While the two IRWs have different rolling radii, they are able to rotate at different rotation speeds without taking an angle of attack or generating a steering force. This feature plays a significant role in IRWs propensity for derailment.

Simulated comparisons

Using NUCARS™ (New and Untried Car Analytic Regime Simulation), researchers at the Transportation Technology Center, Inc., looked at the effect of IRWs on flange climb under two representative LRVs. LRV1 included two articulated car bodies with three trucks (one beneath the articulation joint). LRV2 included three articulated car bodies with a center truck under the middle of the shorter center car body—a common low-floor arrangement. Performance of the vehicles, which used the same wheel (and rail) profiles, was modeled entering a 5-degree curve with 2 inches of superelevation with combined crosslevel, lateral alignment and gauge deviations in the body of the curve. Both vehicles were simulated with conventional rigid axle wheelsets on all three trucks, and with IRWs on the center truck.

While both types of wheelsets see the same external lateral and vertical forces, and both types generate lateral creep forces relating to angle of attack, only the conventional rigid-axle wheelsets generate longitudinal creep forces and, therefore, a yaw (steering) moment.

IRWs, on the other hand, generate no longitudinal forces and, therefore, no yaw, or steering, moment. While this produces a vehicle that will not hunt, it destroys the feedback mechanism that enables the wheelsets to self-steer. As a result, trucks with IRWs tend to operate with higher angles of attack, with no longitudinal force to assist in reducing the lateral flange climbing force. “This results in much shorter wheel climb distances,” Elkins said.

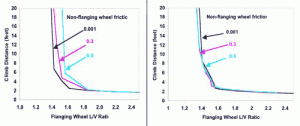
Figure 1 shows the distance it takes the flanging wheel of a conventional wheelset (left) to climb as a function of angle of attack and the COF on the non-flanging wheel. The Figure shows that the IRW behavior is similar to a conventional wheelset with very low friction on the non-flanging wheel. It also indicates that the distance to climb for the IRW is unaffected by the COF on the non-flanging wheel—even at very high friction levels.

“The lower the COF on the non-flanging wheel, the more the rigid axle behaves like an IRW set,” Elkins said. The reason for this is that if the COF on the non-flanging wheel is reduced to almost nothing, the longitudinal force on that wheel is destroyed. The absence of a longitudinal force on the flanging wheel is a primary reason why an independently rotating wheel is more likely to derail, he said.

Figure 2

When these vehicles were run through the simulated curve, LRV2 (the low-floor, three-car body system) produced much higher L/V ratios than the other vehicle. As Figure 2 indicates, LRV2 with IRWs (shown in blue) derailed at 45 mph, just above the Nadal’s value, while the same vehicle with solid axles (shown in purple) operated well above Nadal’s value without derailing. The reason for this is that the solid axles applied a longitudinal force, but the IRWs did not.

LRV2 also produced much higher L/V ratios than LRV1. This occurs because no steering moment is produced when the independently rotating wheelset is pushed into flange contact. A conventional wheelset, conversely, tries to steer itself back to reduce the angle of attack. “As you push it into flange contact, there is a large increase in the rolling radius of the flanging wheel and that tries to pull it around to reduce the angle of attack,” Elkins said. But with IRWs, that effect doesn’t occur. “When you push it into flange contact, there is no moment trying to reduce the angle of attack. So you get a much higher angle of attack.”

Vehicle and wheel profile design

These simulations indicate that vehicle design can have a significant effect on the potential for flange climb derailment, and that articulation and suspension systems must be carefully designed to work with IRWs. They also indicate that wheel profiles can also play a role in a wheelset’s ability to resist derailment.

Longitudinal steering forces are a function of rolling radius difference between left and right wheels. The larger the rolling radius difference, the larger the steering forces. Wheel/rail conicity also plays a role.

A wheelset shifts laterally to equalize the paths traveled by the inner and outer wheels. This lateral shift is inversely proportional to wheelset conicity, Elkins said. Wheel taper and conicity also play a role in wheelset steering and flange contact in curves. Wheels with a 1: 40 taper (0.025 conicity) can negotiate no more than a 1-degree (approximately 5,800-foot radius) curve without making flange contact. Wheels with a 1: 20 taper (0.05 conicity) can accommodate a 2-degree (approximately 2,800-foot radius) curve before making flange contact. Whereas some custom wheel profiles (with 0.2 conicity) can accommodate a 580-foot radius curve before making flange contact.

Like wheel-flange angle, the wheel profile can represent a significant factor in flange climb derailments, Elkins said. “If you’re not in flange contact, you can’t have a flange-climb derailment.”

This article is based on “Wheel/Rail Interaction: Flange Climb Derailment and the Effects of Independently Rolling Wheels,” a presentation by Nicholas Wilson, Scientist – Transportation Technology Center, Inc., and John Elkins, President of RVD Consulting, Inc., at Interface Journal and Advanced Rail Management’s Rail Transit ’04 Wheel/Rail Interaction Seminar.